



上一篇文章里我们解释误导99%发烧友的,关于小空间放不了超低频的问题是,是因为他们只关注到声波在空间里传播的三种研究方法的前两种:几何声学法、统计声学法,而这两种方法,都是以忽略声**动性的。而第三种方法:波动声学法一直在被忽略,然后低频主要研究方法就是波动声学法。接下来我们从波动声学法里的一个关键小项,房间模式和驻波来再深入一下。
房间的比例和大小不同,就会有不同的共振模式。矩形(长方体、正方体)的共振模式比较容易理解
计算和模拟,但歪瓜劣枣的异形空间的共振驻波模式就比较难预测了。对于不规则房间,古老的作法是缩尺法建立一个等比例的模型。在现在,则可以用声学软件来模拟,但这些模拟,都还以忽略尺寸的偏差及材质的阻尼和吸声系数的。所以还是会有比较大的误差。在新式建筑里,为了追求视觉上的标新立异,建筑师们会搞出很多新潮的造型,而对于声学工作者,如果有机会可以选的话,肯定是更希望选长得规矩些的空间来作声学设计。但是能按期望进行土建的空间实在太少,对于建好的建筑,特别是阁楼,我们基本没有选择的权利,我们必须学会应付各种形状的空间。

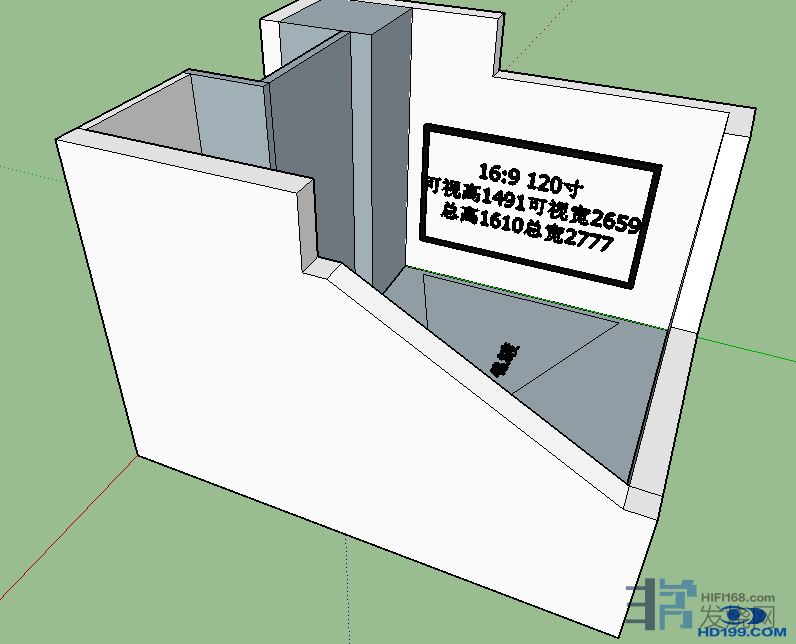

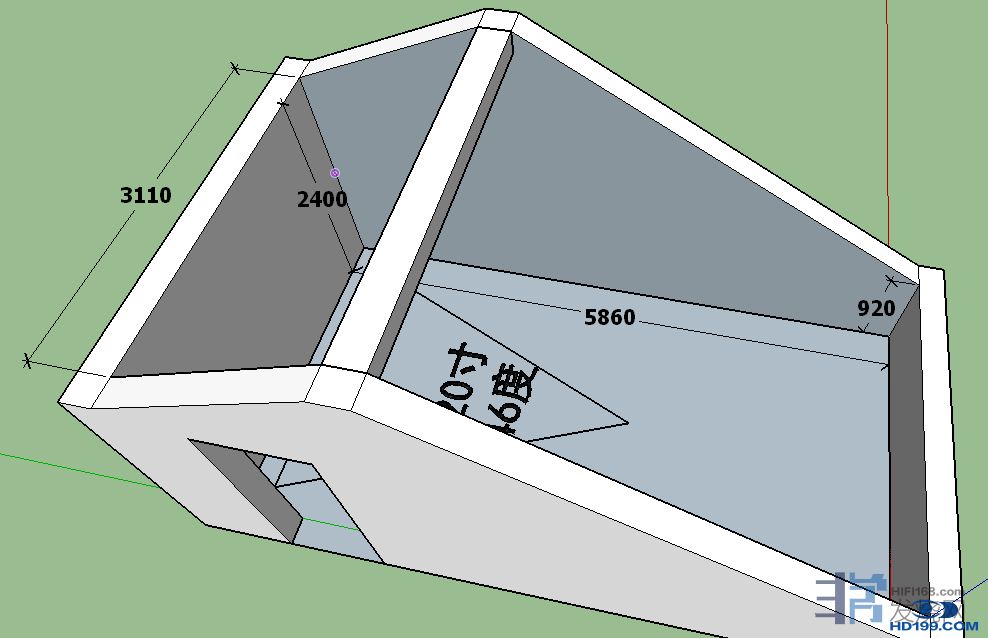



在两个平行面之间,驻波是这样形成的。当某个频率的声音波长的一半恰好等于两平面之间距离的整数倍时, 就会产生共振和驻波现象。这被称为轴向模式, 因为它们都是沿矩形房间内的主要轴向方向长、宽、高而存在。

而房间典型的房间模式除了上面图上算的轴向之外:还有斜向和切向共3种。
那是否可以对对房间的形状和尺寸进行优化?
我们可能会幻想,如果能避免房间有平行边界的出现,是否房间共振模式就不存在了呢。很遗憾,并不是这样的。小范围的打破声学平行面,对中高频的反射有些作用,所以看到很多录音室都有打破平行面。但对超低频的驻波模型的改变是很小的,然而,声源的位置和吸声材料的分布也是共振模式中重要的因素,非矩形的房间形状有助于共振阻尼更加平坦。然后非矩形房间的声音表现是很难预测的,除非我们拥有足够精确的模型和强大的计算机。
因此,声学科学家们更加偏爱简单的矩形。那么现在问题就变成了: 什么样的矩形是最佳的选择?世界各不同的科学家提出了不同的最佳比例,但基本达成共识的一种普遍的观点认为,应该使房间共振模式的分布更加均匀,而尽量避免重叠和大低谷。房间的尺寸决定了共振频率本身, 而决 定共振频率分布情况的, 却是房间的长宽高之间的比例。避免使用简单正方形或 是长宽高之间呈简单整数倍关系的房间已经成为惯例,因为这样会使共振峰的频率比较接近,能量消散慢的频段叠加堆积在一起。 多年以前, 人们就通过多方努力来寻找最优的混晌室的边长比例,在这里,共振频率的分布均匀是很重要的,因为要在这里测量机电设备的声功率输出。 将上述观点引人音频领域,人们会建造特定边长比例的房间,因为它们具有优秀的听觉特性。在普通房间内,这样的好处仅限于低频段。Bolt ( 1946 )因 为其提出的“波尔围线”而闻名,就是用这样独特的方式,更加清晰地指明什么样房间三边比例是更优化的,并画出了“有效范围”。

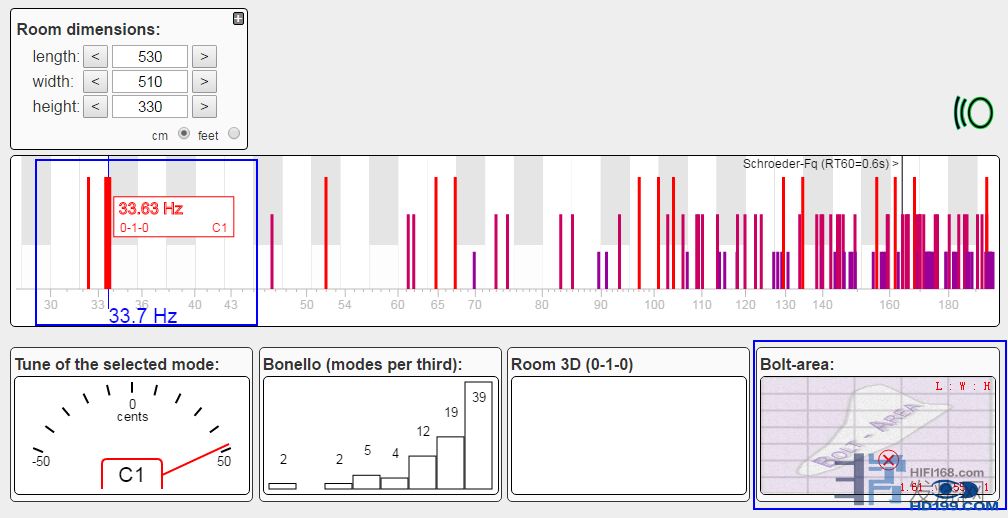
计算机软件模拟的房间驻波因为算法是基于理想化的情况,所以许多人会毫不怀疑地将计算出来的共振频率与房间里我们测得的紧密关联在一起,一般情况下,这种验证是能得到大方向上的一致,但很多时候,也会出现明显的不吻合,关于此,有很多解释,但最常提到的就是家庭空间与“理想矩形”的差距,理想概念中的房间具有完全反射边界例如硬砖墙,而现实中的房间,可能有剪力墙、预制板、隔墙、木板、石膏板等,还有门窗洞和家具软装,这些就会导致软件模拟出现极大偏差,同时软件对异形的模拟偏差就更大了。
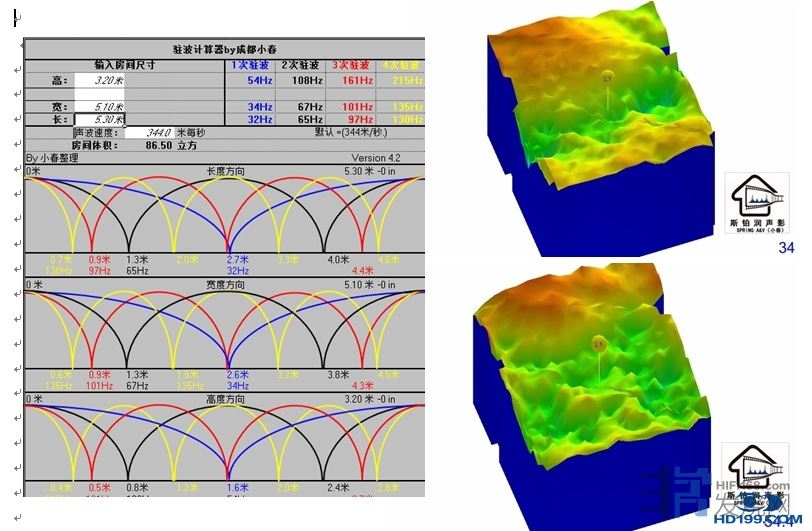
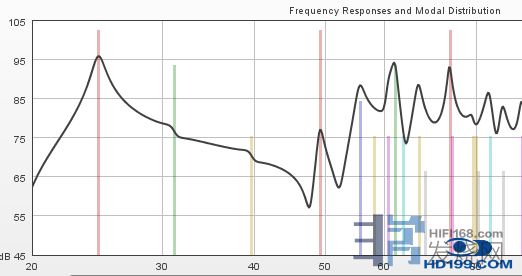
例如对一个长6.97宽5.51高3.08的房间作模拟的结果:

而实测实物声学处理后的结果:

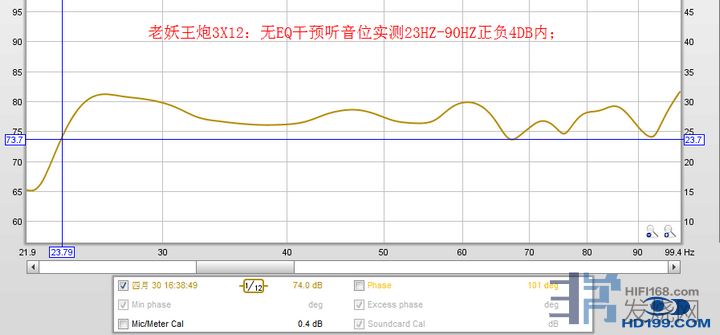




从实测的结果我们可以看出,声学处理会极大的改变模拟的结果,并且这还是只有一只炮的情况下,如果是还有多炮加上异形的情况下,计算机几乎就无法模拟了。
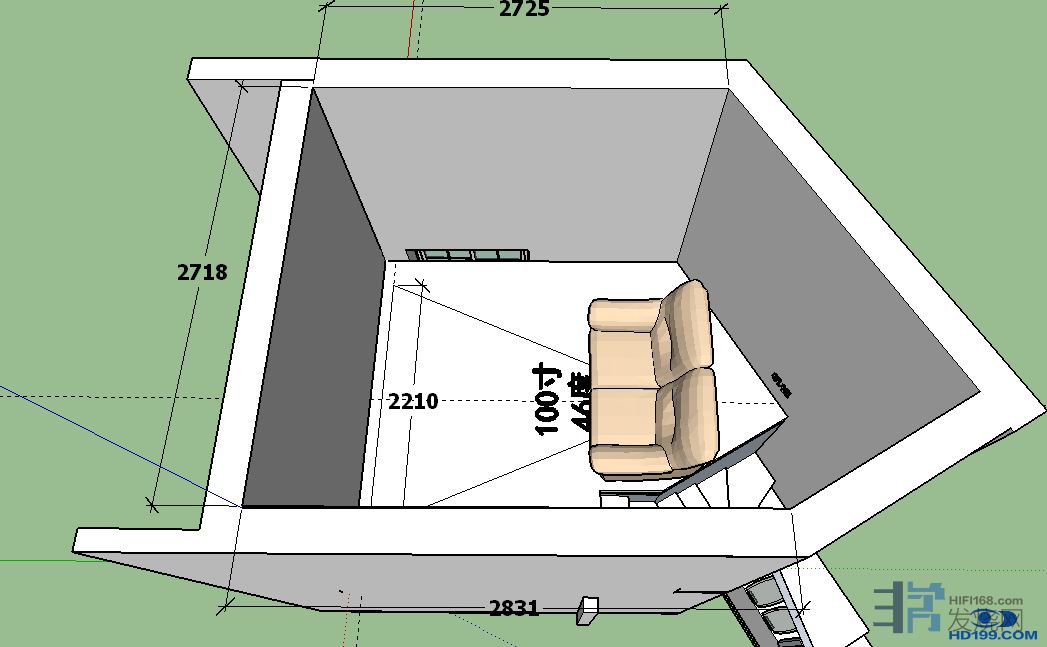
例如这样一个长8.56宽主箱后方5.59高主体2.68的异形空间:

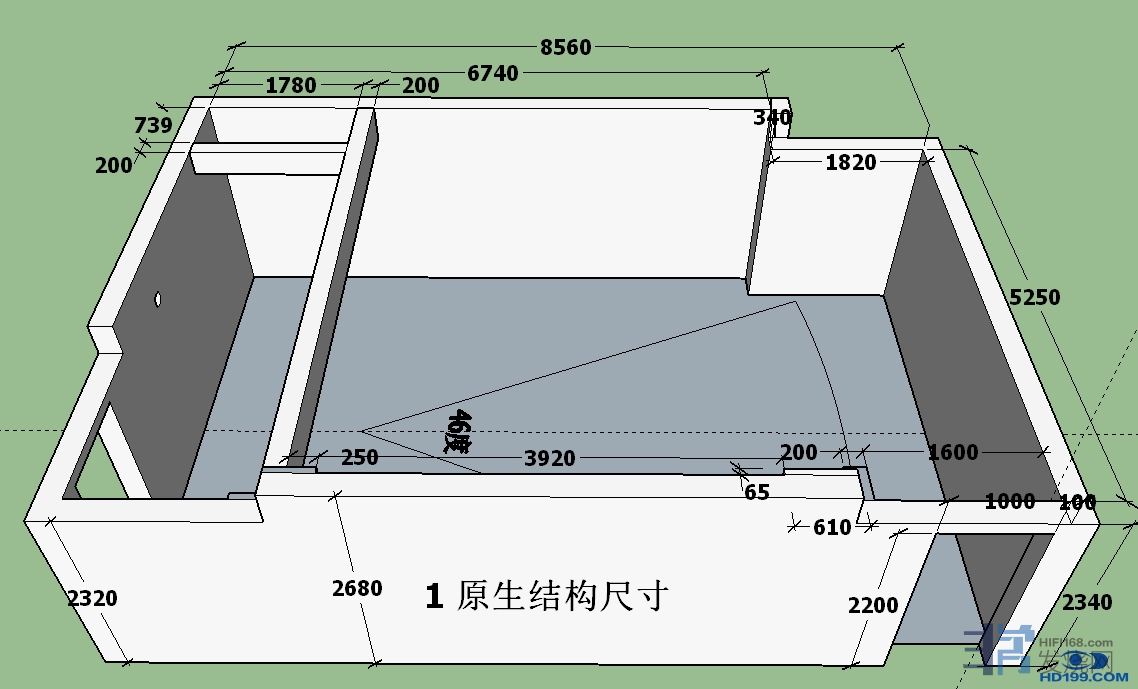

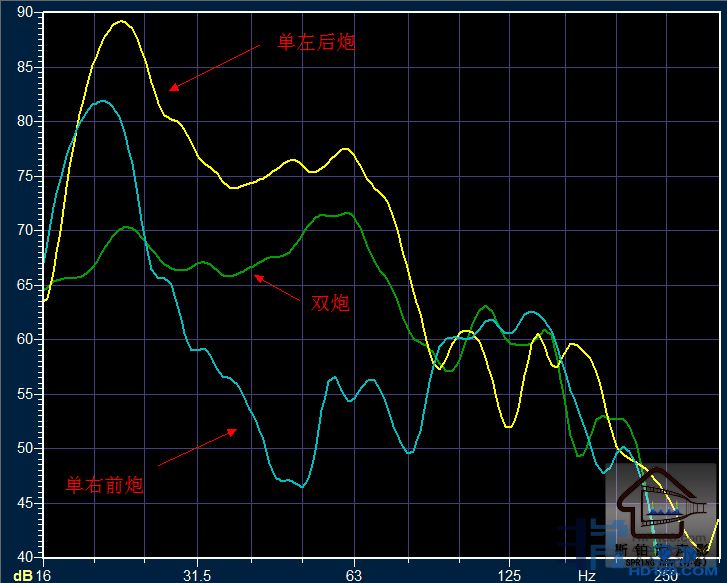
总结一下,我们发现要想降低房间内听音区的驻波,使用多只超低音 扬声器是有正面意义的。然而还有一些要点我们需要:
1.模拟对于规整矩形有一定的参考意义,2.一些比较优秀超低频频响且能量快速消散对空间声学依赖是巨大的;3.多炮可以在一定程度对驻波进行抑制,4.房间比例仍然是要考虑的因素。5.适当不滥用均衡器也不应该排斥。所以上述结论,都是广泛性的结论,并不存在某一种能适合任何结构的方案。